Berechnung von Planetenbewegungen

Kreisbahnen

Für Venus, Erde und Neptun ist die Kreisbahn eine recht gute Näherung.
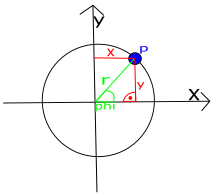Die Position eines Punktes P auf einer Kreisbahn kann man in kartesischen Koordinaten (x, y) aber auch in Polarkoordinaten angeben (r, φ) angeben, wobei r der Radius und φ („phi“) der Winkel zu x-Achse ist.

Es gilt: x = rcos(φ), denn cos(φ) = x/r, außerdem gilt: y = rsin(φ), denn sin(φ) = y/r
Auf einer Kreisbahn hat ein Planet wegen der Drehimpulserhaltung eine konstante Winkelgeschwindigkeit:
ω(„omega“) = φ/t, also φ = ωt
also gilt x = rcos(ω t) und x = rsin(ω t)
mit ω = v/r = √(GM/r)/r = √(GM/r³), was man auch im Gravitationsgesetz sehen kann.
kennt man die Umlaufzeit, dann verwendet man ω = 2π/T
also x = rcos(2π/Tt) und x = rsin(2π/T*t).

Excel Tabelle mit dem Beispiel der Erde

Ellipsenbahnen

Nach dem ersten Kepler-Gesetz bewegen sich die Planeten auf einer Ellipsenbahn um die Sonne.
Die Position eines Planeten auf seiner Bahn wird wieder in Polarkoordinaten
r: Abstand zur Sonne (in Astronomischen Einheiten(1 AE = Abstand Erde – Sonne))
ν(„ny“): wahre Anomalie
angegeben.

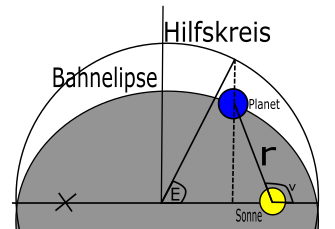
Es gilt r = a(1-ecos(E))
tan(ν/2) = √(^1+e/_1-e)tan(E/2), oder umgeformt ν = arctan(„Umkehrfunktion zu Tangens“)((^1+e/_1-e)tan(E/2))
mit a(„schon vorher gegeben“): große Halbachse der Ellipse
und e(„schon vorher gegeben“): numerische Exzentrität („legt die Bahnform fest“)

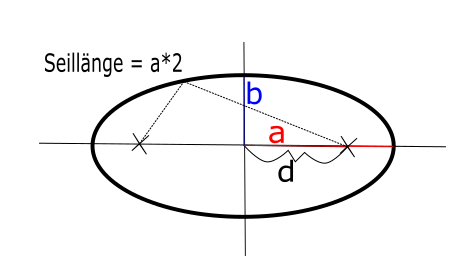
e = d/a und 0 kleiner e kleiner 1
E = exzentrische Anomalie (im Bogenmaß angegeben)
Die exzentrische Anomalie wird aus der Kepler-Gleichung:
E-e*sin(E)=M („in Bogenmaß“) (das Problem an der Formel ist, dass sie nur von einem Computerprogramm ausgerechnet werden kann)
mit Hilfe der Fixpunktiteration des Newtonverfahrens aus e und M berechnet.
Die mittlere Anomalie wird in Abhängigkeit von der Zeit t berechnet:
M = (^2π/_T)(t-to) mit T = Umlaufzeit des Planeten und to = Zeitpunkt des Periheldurchgangs

ist T gegeben kann man jetzt für jeden Zeitpunkt t die Position des Planeten auf seiner Ellipsenbahn berechnen.
Excel Tabelle mit dem Beispiel des Merkurs